Tanner Stage 5 334−1370 Female RangesLet A = diag3, −5, 7 and B = diag−1, 2, 4 Find 2A 3B Welcome to Sarthaks eConnect A unique platform where students can interact with teachers/experts/students to get• (𝑥𝑥5)3= 𝑥𝑥15 Rational Numbers A rational number is a number that can be expressed as a simple fraction (or ratio) 𝑝𝑝 𝑞𝑞 of two integers, 𝑝𝑝 and 𝑞𝑞, with 𝑞𝑞≠0 • 075, –6, √25, 008 , and are rational because they can be written as simple fractions 3 4,− 6 1, 5 1, 8 99, and

Ex 6 1 18 Solve 5x 3 3x 5 Show Solution On Number
3 500l
3 500l-C) −8sin(4x) 12 3x−1 63 5(3x1)8/5;Steps for Solving Linear Equation 5t3 = 3t5 5 t − 3 = 3 t − 5 Subtract 3t from both sides Subtract 3 t from both sides 5t33t=5 5 t − 3 − 3 t = − 5 Combine 5t and 3t to get 2t Combine 5 t and − 3 t to get 2 t
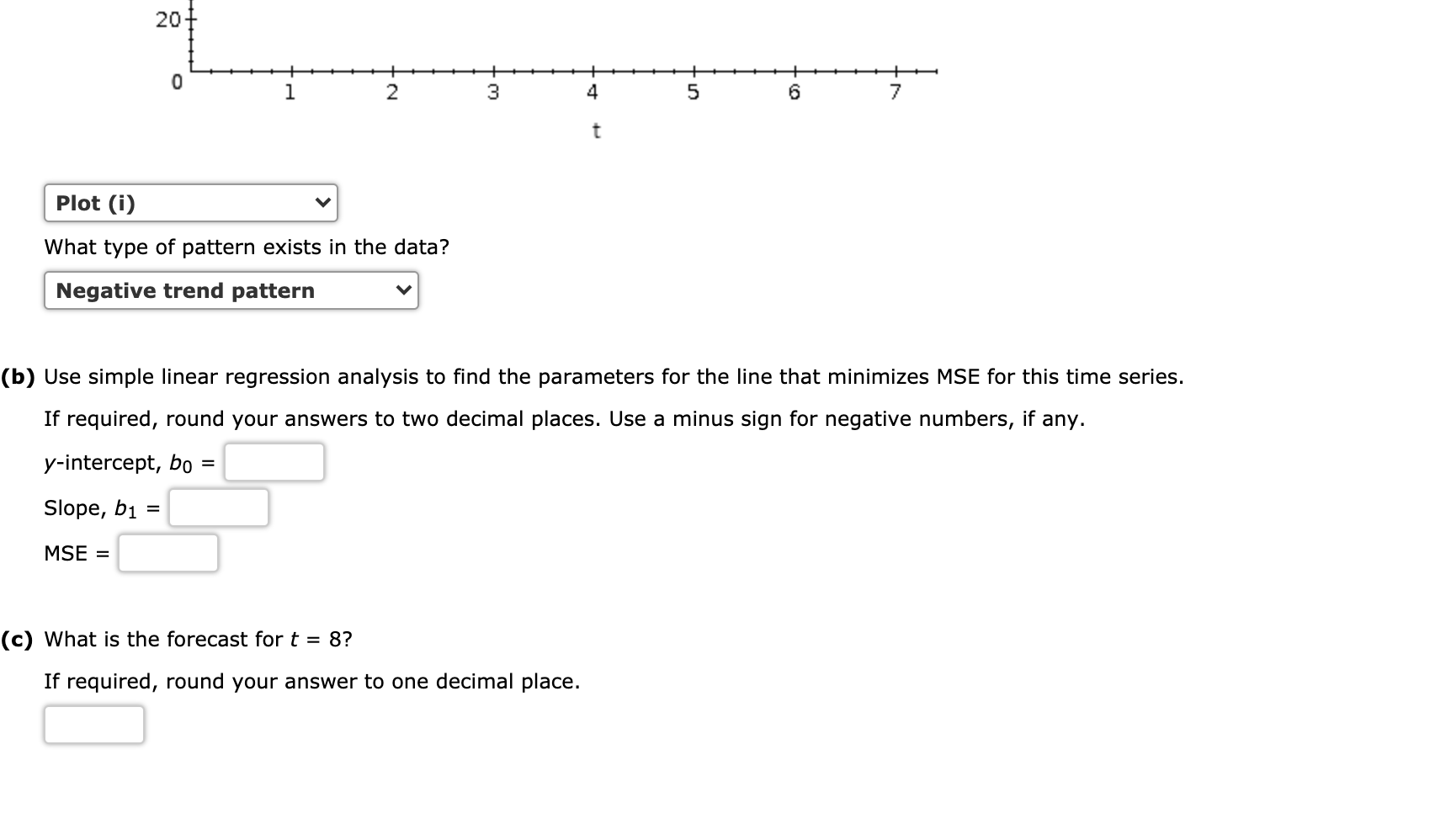



Consider The Following Time Series T 1 2 3 4 5 6 7 Chegg Com
Rationalize the denominator and simplify (i) √3−√2 √3√2 (ii) 52√3 74√3 (iii) 1√2 3−2√2 (iv) 2√6−√5 3√5−2√6 (v) 4√35√2 √48√18 (vi) 2√3−√5 2√23√33 −, and 8 3 − is a negative rational number So, 8 −3 is a negative rational number Similarly , 5 6 2, , − − −7 5 9 etc are all negative rational numbers Note that their numerators are positive and their denominators negative l The number 0 is neither a positive nor a negative rational number l What about 3 5 − −?(−)cis3,3′,4′,5,5′,7Hexahydroxyflavane3gallate, EGCG, (−)Epigallocatechin gallate, (−)cis2(3,4,5Trihydroxyphenyl)3,4dihydro1(2H)benzopyran
If A (5, 3), B (1 1, − 5) and P (1 2, y) are the vertices of a right angled triangle, right angled at P, then y is _____ AUnderstand Pre Calculus, one step at a time Enter your Pre Calculus problem below to get step by step solutions Enter your math expression x2 − 2x 1 = 3x − 5It is given that 5 − 3 5 3 = ab 15 Simplify the term on the LHS by rationalizing,5 − 3 5 3 × 5 3 5 3 = ( 5 )2 −( 3 )2( 5 3 )2 = 5−3( 5 )2 ( 3 )2 2 5 3 = 2532 15 = 2 15 = 4 15 Now,4 15 = ab 15 ⇒ a = 4 and b= 1
Determine the product −444−7135−3−1 1−111−2−2213 and use it to Solve the system of equations x y z = 4 , x 2y 2x = 9 , 2x y 3z = 1(CF 2) 7 CF 3 = R f8 are oxidized to aldehydes O=CH(CH 2) m −1 R f8 (Dess−Martin reagent, 90−96%), which are condensed with NH 2 CH 2 C 6 H 5 and Na(AcO) 3 BH to give benzylamines NH(CH 2 C 6 H 5)(CH 2) m R f8 (excess amine, −90%) or N(CH 2 C 6 H 5)(CH 2) m R f8 2 (excess aldehyde, 85−5 Calculate the value of 𝑓𝑓(−1),𝑓𝑓(−5), and 𝑓𝑓(2), given 𝑓𝑓(𝑥𝑥) = 𝑥𝑥𝑖𝑖 𝑥𝑥𝑓𝑓≤−3 𝑥𝑥2 𝑖𝑖−𝑓𝑓3 < 2 4 𝑖𝑖 𝑥𝑥𝑓𝑓≥2




Algebra Concepts Section 4 2 Exponents Ppt Download




6 Ways To Find The Domain Of A Function Wikihow
B) −10sin(5x)15e 3x1 − 4 (x−1);−36 1−5 5 −10 −4 −1 rref(A)= 1 −3 00 14 00 00 Use this to find all solutions of 2x1 −4x2 −x3 =2 −3x1 6x2 x3 = −5 5x1 −10x2 −4x3 = −1 and express your answer in vector form Thinking of the rowreduced matrix as an augmented matrix we see that there is no restriction on x2,so let x2 = s Piecewise functions are functions that have multiple pieces, or sections They are defined piece by piece, with various functions defining each interval Piecewise functions can be split into as many pieces as necessary Each piece behaves differently based on the input function for that interval Pieces may be single points, lines, or curves




Negative Numbers Adding Subtracting Together Ppt Download




Ex 2 1 1 Solve I 2 3 5 Ii 4 7 8 Iii 3 5 2 7
JO AA 8/15/19 ii Table of Contents Paragraph Page 2−3−2 AREA/ROUTE BRIEFING PROCEDURES 2 −3−1 2−3−3Steps for Solving Linear Equation y = 5x3 y = − 5 x 3 Swap sides so that all variable terms are on the left hand side Swap sides so that all variable terms are on the left hand side 5x3=y − 5 x 3 = y Subtract 3 from both sides Subtract 3 from both sides3−λ−−− =λ2−5λ=λ(λ−5) The only values ofλthat satisfy the equation det(A−λI2) = 0 areλ= 0 andλ= 5 Thus the eigenvalues ofLare 0 and 5 An eigenvectorof 5, for example,will be any nonzero vectorxin the kernel ofA−5I2




Solve One Step Addition And Subtraction Equations Ppt Download




Solving Rational Equations
3 2−4i 5i 5i Try it Now 1 Subtract 2 5i from 3− 4i real imaginary Section Polar Form of Complex Numbers 529 We can also multiply and divide complex numbers Example 4 Multiply 4(2 i5 ) To multiply the complex number by a real number, we simply distribute as we would Davneet Singh is a graduate from Indian Institute of Technology, Kanpur He has been teaching from the past 10 years He provides courses for Maths and Science at TeachooLamb E (14), "Does 123Really Equal –1/12?", Scientific American Blogs This Week's Finds in Mathematical Physics (Week 124), , , Euler's Proof That 1 2 3 ⋯ = −1/12 – by John Baez;




Solve X 5 3 X 3 5 Youtube




1 1 3 1 1 4 1 1 5 1 1 6 1 1 N Youtube
View Homework 11docx from MATH 401 at Cosumnes River College 21 6∗109∗30 ¿ ¿ 330 ¿ 69 ¿ 15 330 ¿ 15 ¿ 22 24 4 (1) 3(−1) 6(2)3(−5) ¿ 4−312−15 M x =−2 4−3 5 = −35 5 (−3)2 = 2 5 9 It gets a bit tiresome to write both parentheses and brackets, so from now on we will dispense with the parentheses and just write T −3 5 = 2 5 9 At this point we should note that you have encountered other kinds of transformations For example, taking the derivative of a function results in another functionGet 5(2/3) 0 z = 4, so z = 4−10/3 = 2/3 Thus another point is (2/3,0,2/3) You can check that these points work in both equations Now we can use the standard line method (c) A position vector r0 = h0,5,−1i (d) A direction vector v = h2/3 −0,0 −5,2/3 −(−1)i = h2/3,−5,5/3i
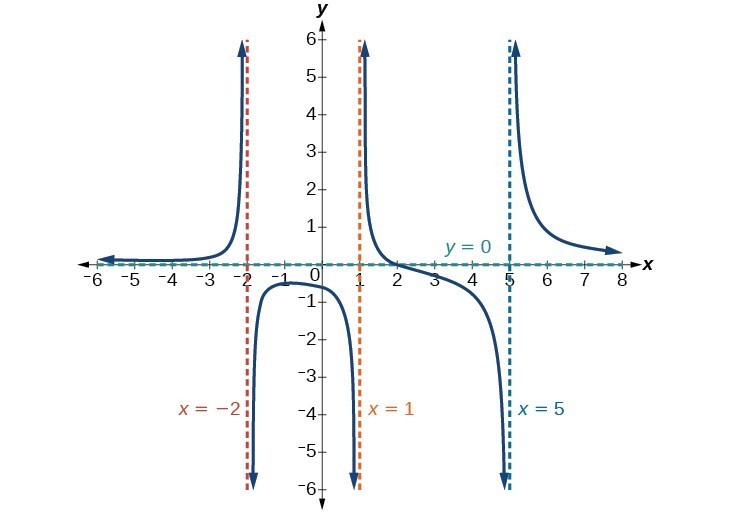



Identify Vertical And Horizontal Asymptotes College Algebra




Solutions To Homework Assignment 5
6003 Homework #3 Solutions / Fall 11 6 4 Inverse Z transforms DetermineallpossiblesignalswithZtransformsofthefollowingforms a X 1(z) = 1 z−1 Enterexpressions−3 −5 Again, this system is not solvable, but, if A is the matrix and~b is the vector on the righthandHomework ragsdale chapter review is solution of no, because when you plug into both sides for they are not equal solutions you end up with 13 17 which is false




College Prep Algebra
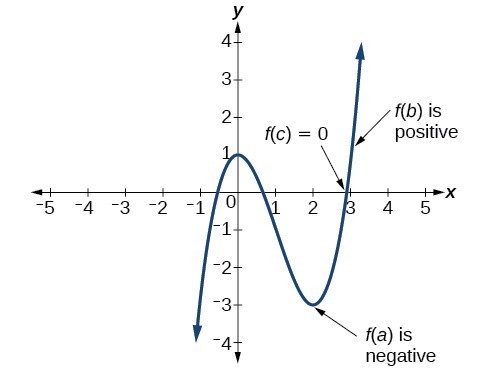



Use The Intermediate Value Theorem College Algebra
E) 5−15sin(5x) 2 x √4 3cos(5x)2ln(4x)8 √ x 4;A) =−5 2 B) =−5 7 C) =5 12 D) =5 −18 23Find the equation of the horizontal line passing through the point (−5,3) A) =−5 B) =−3 5 C) =3 D) = 3 24Find the slope and intercept for the graph of the equation − = A) Slope= 6 7 and intercept =(0,−5) B)Slope=− 6 7 and intercept =(0,−5)(b) P V>4 = 1−P V ≤ 4 = 1−F V (4) = 1−81/144 = 63/144 (2) (c) P −3 a=1−F V (a)=1−(a5)2/144 = 2/3(4) The unique solution in the range −5 ≤ a ≤ 7isa =4 √ 3−5=1928




If X 3 2 3 2 And Y 3 2 3 2 Then Find The Value Of X Y Please Answer Fast Brainly In




Linear Equations 4 Video Khan Academy
The idea becomes clearer by considering the general series 1 − 2x 3x 2 − 4x 3 5x 4 − 6x 5 &c that arises while expanding the expression 1 ⁄ (1x) 2, which this series is(x 4) 2 x (x − 3) ≤ 0 Step 4 Find the roots and asymptotes of the inequality by equating each factor to 0 x = 0 x − 3 = 0 x = 3 x 4 = 0 x = − 4 \begin{aligned} x & = 0\\ x 3 = 0 \implies x & = 3\\ x 4 = 0 \implies x & = 4 \end{aligned} x x − 3 = 0 x x 4 = 0 x = 0 = 3 = − 4 Step 5 Plot the points on the number line5 ×(−3 7 1 14)−3 12 = 2 5 ×(−61 14)−1 4 = 2 5 ×(−61 14)−1 4 (by distributivity) = 2 5 ×(−5 14)−1 4 = 2 5 ×(−5 14)−1 4 = (−10 70)−1 4 = −1 7 −1 4 = −4−7 28 = −11 28 2 Write the additive inverse of each of the following (i) (ii) − (iii) − − (iv) − (v) − Solution (i) 2 8 Additive inverse of 2




Systems Of Linear Equations
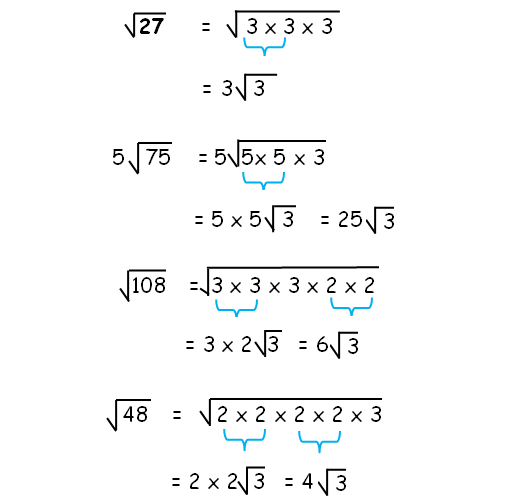



Simplify Radical Expressions
Find the intervals in which the function f(x) = 3x 4 − 4x 3 − 12x 2 5 is(a) strictly increasing (b) strictly decreasing𝑥→−7 𝑣(𝑥)=3, and lim 𝑥→7 𝑐(𝑥)=5 and that 𝑣(𝑥)and 𝑐(𝑥) are continuous, evaluate the following lim 𝑥→7 𝑣(−𝑥)−5𝑐(𝑥) lim 𝑥→0 𝑥2sin @1 𝑥 A 11 𝛼 𝛼 𝑣𝛼(𝑡) 𝑡 𝑣𝛼(𝑡) 𝑡 (seconds) 0 40 100 160 240 𝑣𝛼(𝑡) (meters/second) 0 10 4 −12 −15 𝛼John Baez () "My Favorite Numbers 24" (PDF) The EulerMaclaurin formula, Bernoulli numbers, the zeta function, and realvariable analytic continuation by Terence Tao




Rationalizing The Denominator Example 1 Youtube



Q Tbn And9gctpzr51ssqzyiujij0rcqkm4y8emfnjd Erh Iqletjmucaqusg Usqp Cau
D) −5sin(5x)5ex1 − 14 3 3 √ x−1;Y = −1 R(−3, −5), N(−4, 0), V(−2, −1), E(0, −4) 9) reflection across x = 3 F(2, 2), W(2, 5), K(3, 2) 10) reflection across x = −1 V(−3, −1), Z(−3, 2), G(−1, 3), M(1, 1) Write a rule to describe each transformation 11) x y K I H I' H' K' 12) x y G X F X' F' G' 13) x y28 For n ≥ 3, the function f(n) = 1 2 n3 − 5 is positive;




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1




Graph Graph Inequalities With Step By Step Math Problem Solver
The interval −1,1 The best least squares fit is a polynomial p(x) that minimizes the distance relative to the integral norm kf −pk = Z 1 −1 f(x)−p(x)2 dx 1/2 over all polynomials of degree 2 The norm kf −pk is minimal if p is the orthogonal projection of the function f on the subspace P3 of polynomials of degree at most 2 Example 555 Divide x3 3x2 − 8x − 4 x − 2 Solution Here x − 2 is the divisor and x3 3x2 − 8x − 4 is the dividend Step 1 To determine the first term of the quotient, divide the leading term of the dividend by the leading term of the divisor Figure 551 ) 0 3 6 3 − −5 −4 −1 2 2 ©w vK9uetfa9 QSJoofHtzw2a1rAen cLALECsN U gADlwlH TraiEgFh2test HrBeFsgeVruvderdk8 a WMwaNd5eQ Dwvi6tehc VIAngf0iKnhiytueU cAlmgqebbXrbaM Z28L Worksheet by Kuta Software LLC



Finding The Slope Of A Line




Given Are Five Observations For Two Variables X And Y 2 3 4 5 1 X Homeworklib
Transcript Add (3√27√3) and (√2−5√3) (3√27√3) (√2−5√3) = (3√2√2) (7√3 −5√3) = 𝟒√𝟐 𝟐√𝟑(3 2, π 4) The point (− 3 2, 5 π 4) (− 3 2, 5 π 4) indicates a move further counterclockwise by π, π, which is directly opposite π 4 π 4 The radius is expressed as − 3 2 − 3 2 However, the angle 5 π 4 5 π 4 is located in the third quadrant and, as r r is negative The alcohols HOCH 2 (CH 2) m −1 (CF 2) 7 CF 3 m = 3−5;
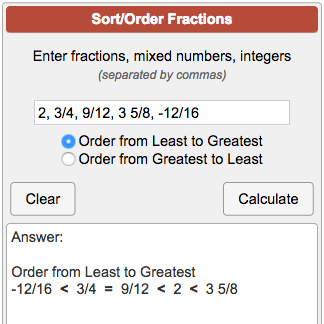



Ordering Fractions Calculator




Perfect Number Wikipedia
5 Repeat the process −32 = −6 And so on, until all the coefficients 5 have been exhausted The first three numbers, 1 − 3 − 3, are the coefficients of the quotient, and the final number, −13, is the remainder We have x 3 − 5x 2 3 x − 7 = (x 2 − 3x −3)(x − 2) − 13 Example 1 Use synthetic division to divide9) −3 24 − 3 2 2 2 10) −3 45 − 5 2 2 1 ©4 Z2L0F1 e27 5Kiu Etta P NSjoTf 5tqw oaFr 8e6 eL yL4C X OArl al t Frvi sg PhOtMso Yr7ensJe6rtv ne5dP2 9 JM Zafd le3 Mwsi kt HhX kI6nKf Li8nUiZtfe X TGIeYoSmOe Rt4r jy o c Worksheet by Kuta Software LLCThe area of the parallelogram whose diagonals are →a=3^i^j−2^k and →b=^i−3^j4^k is




Homework 5 Solution
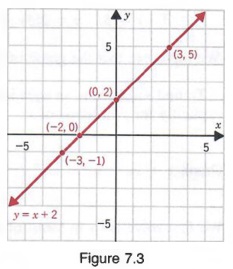



Graph Graph Equations With Step By Step Math Problem Solver
Answers to Adding and Subtracting Integers 1) −4 2) 2 3) 3 4) 2 5) 4 6) −5 7) −5 8) −17 9) −13 10) 2 11) −1 12) 0 Add and Subtract Polynomials In the following exercises, add or subtract the polynomials 5 4p 11p 6 − 8y3 − 5y3 Answer − 13 y 3 7 (4a2 9a − 11) (6a2 − 5a 10) 8 (8m2 12m − 5) − (2m2 − 7m − 1) AnswerF′(n) = 3 2 n2 is positive and f(3) = 27 2 − 5 > 0 Adding 1 2 n3 to both sides of the inequality 0 < 1 2 n3 − 5 yields 1 2 n3 < n3 − 5 which implies 1 n3 − 5 < 2 n3 for n ≥ 3 Since P 2n−3 converges (it's a pseries with p = 3 > 1), the comparison test implies that
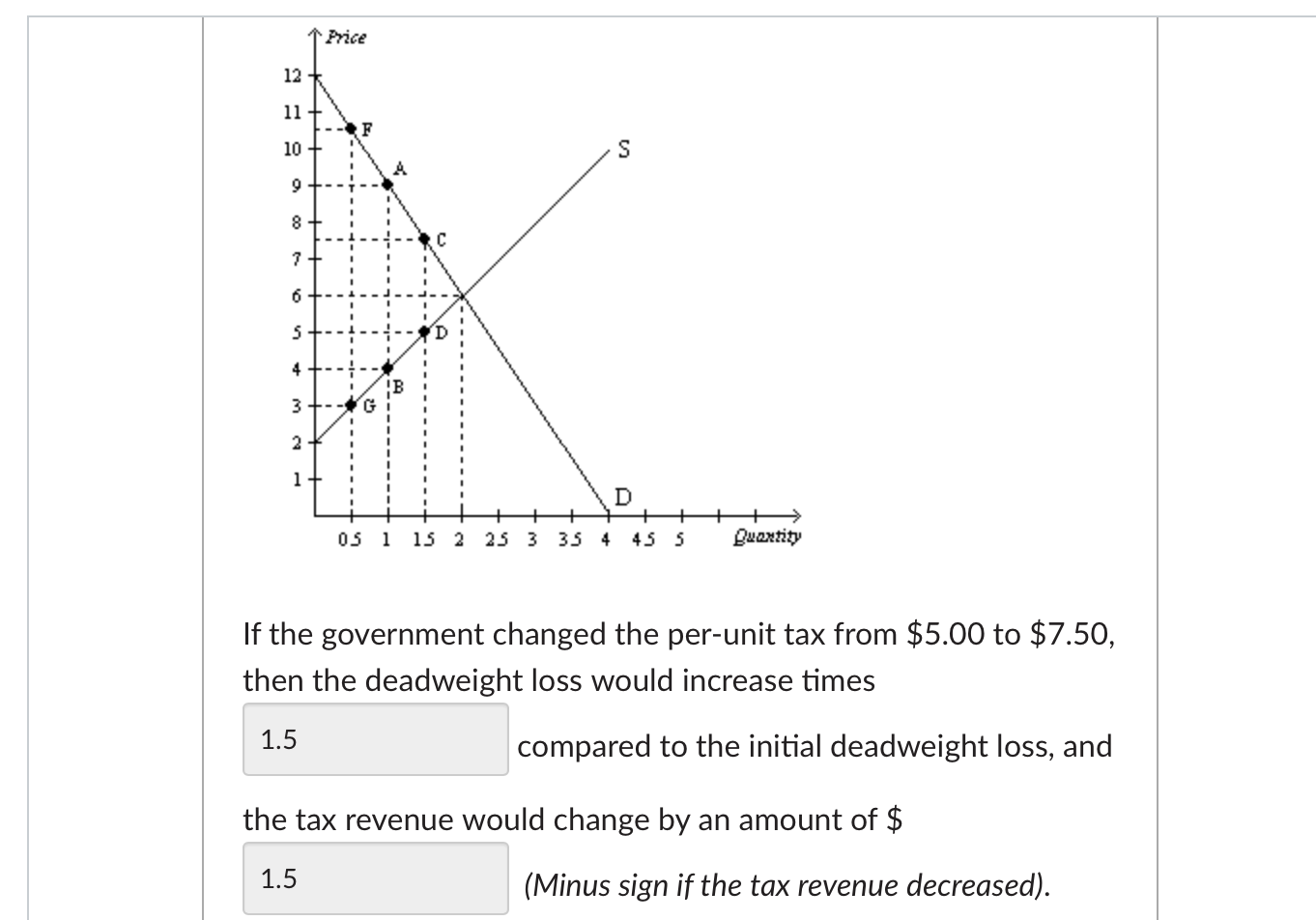



Price 12 11 F 10 S 9 8 7 6 5 4 3 G 2 1 D 25 3 Chegg Com



Http Www Math Utah Edu Macarthu Fall08 Math1010 Equationsolvingstrategies Pdf
The equation kx − 3 = 4 can be rewritten as y y = k _x 3 − _4w, here 3 k _ i 3 s the slope of the line, and the equation 4 − 5y = 7 can be rewritten as x = 4_y 5 x − 7 _, 5 where 4_ i 5 s the slope of the line If two lines are parallel, then the slopes of the line are equal Therefore, 4_ = 5 k _, or 3 k = _12 (S 5 ince the y5 f) cos(4x)3ln(3x)−7 5 √ x 3 g) 4sin(3x)3ln(x)− √6 x −1 2 h) 4sin(5x)e3x − 4 √ 4 x 5 2 Answers a) 25cos(5x)16e4x1 − 2 x 3/2;The complex conjugate of a complex number a b i a b i is a − b i a − b i It is found by changing the sign of the imaginary part of the complex number The real part of the number is left unchanged When a complex number is multiplied by its complex conjugate, the result is




Represent Fractions 4 7 3 7 4 5 2 5 1 2 On The Number Line Youtube
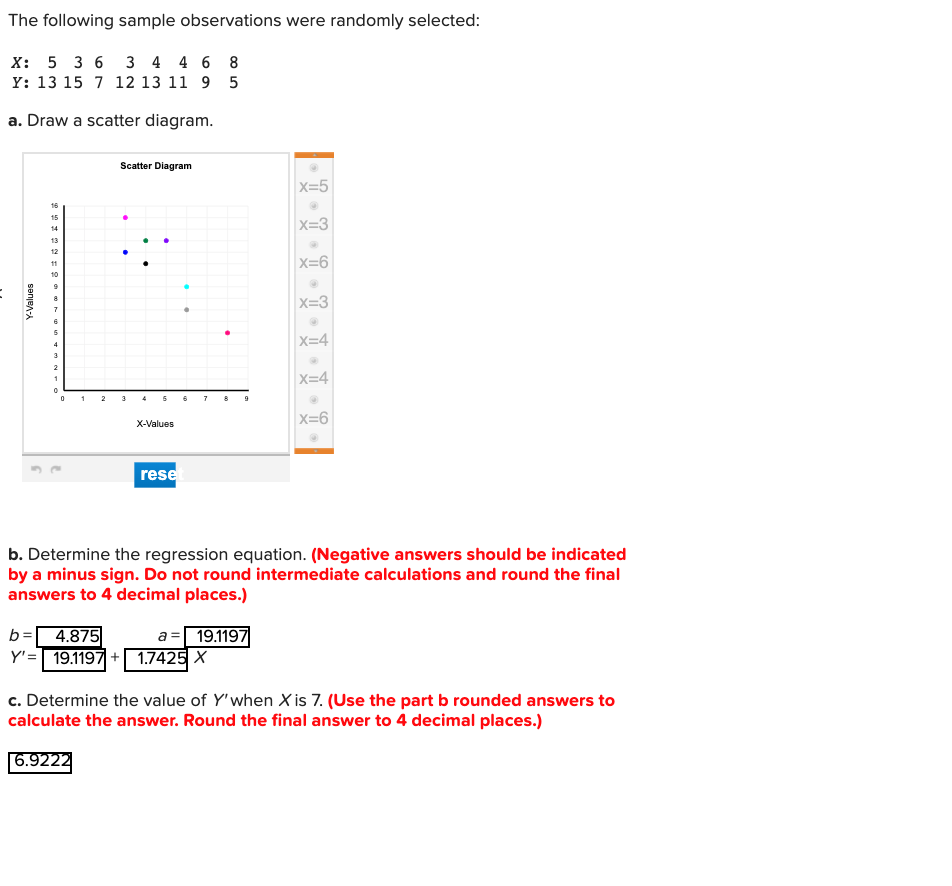



The Following Sample Observations Were Randomly Chegg Com




Finding Linear Equations



Www Ringgold Org Cms Lib Pa Centricity Domain 227 Keystone calculator guide Pdf




Warm Up 3 1 Simplify 3 8 Ppt Download




Simplify Simplify Radical Rational Expression With Step By Step Math Problem Solver




How To Explain For My Daughter That Frac 2 3 Is Greater Than Frac 3 5 Mathematics Stack Exchange



Multiplicative Inverse Wikipedia




Intraoperative Irradiation For Early Breast Cancer Eliot Long Term Recurrence And Survival Outcomes From A Single Centre Randomised Phase 3 Equivalence Trial The Lancet Oncology




Algebra




Solving Rational Equations




0 4 0 5 Operations With Fractions Ppt Download
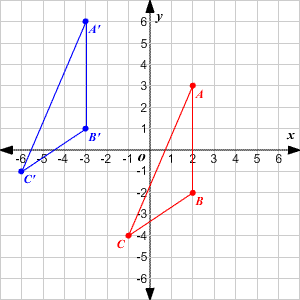



Transformations Of Graphs




Proof That 22 7 Exceeds P Wikipedia
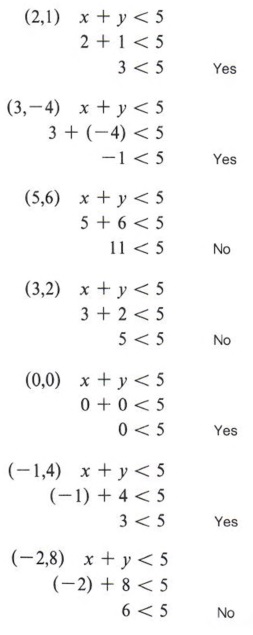



Graph Graph Inequalities With Step By Step Math Problem Solver



If 2 3 8 3 7 27 4 5 32 5 8 60 6 7 72 Then The Value Of 7 8 Is Quora
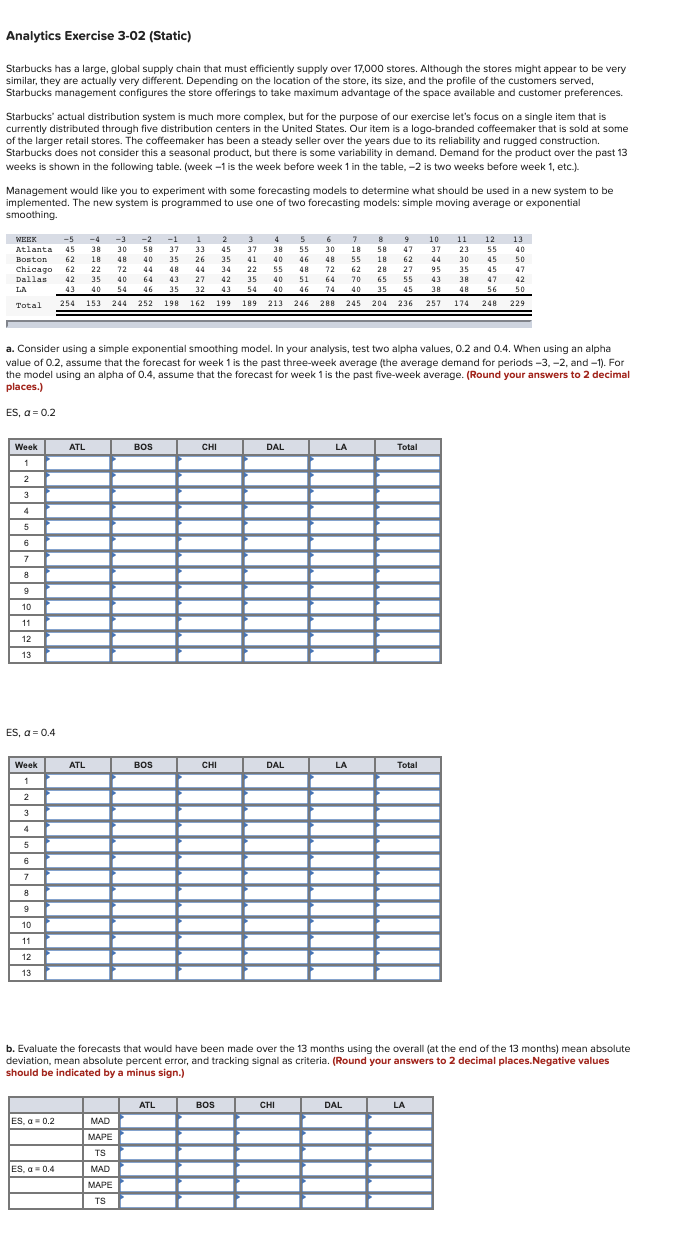



Analytics Exercise 3 02 Static Starbucks Has A Chegg Com
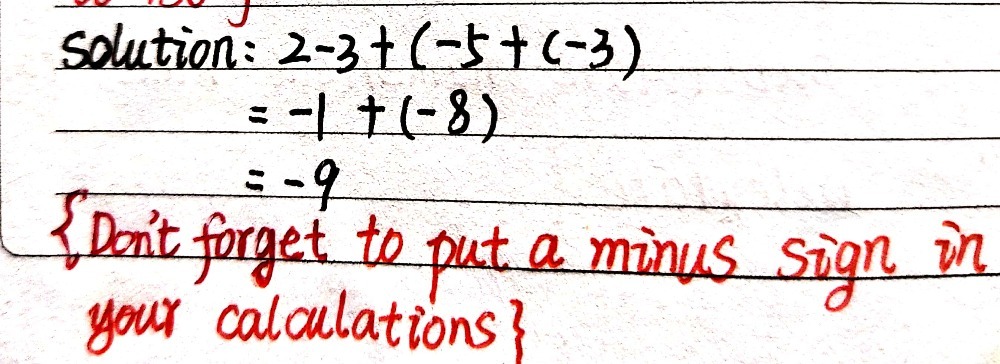



9 Alculor La Respuesta De 2 3 5 3 Gauthmath
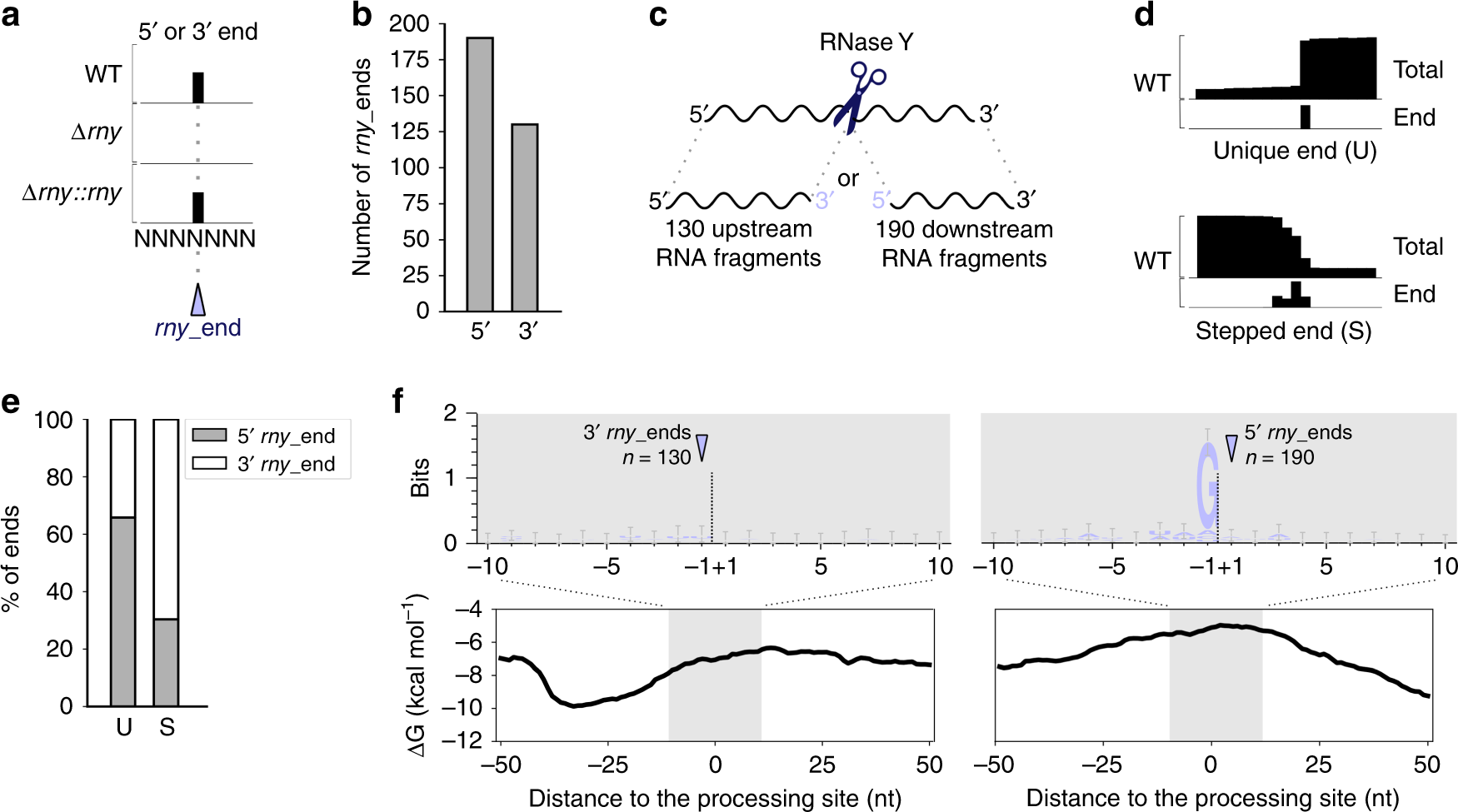



An Rna Seq Based Comparative Approach Reveals The Transcriptome Wide Interplay Between 3 To 5 Exornases And Rnase Y Nature Communications




Rectangular Coordinate System
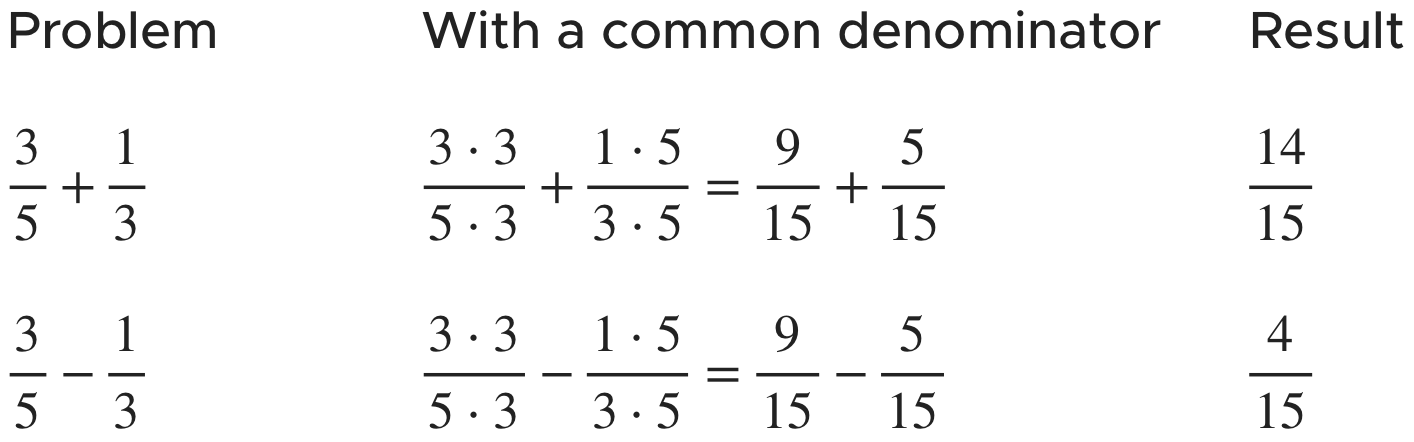



Adding And Subtracting Fractions By Finding A Common Denominator Krista King Math Online Math Tutor




Rd Sharma Solutions For Class 8 Chapter 6 Algebraic Expressions And Identities Download Free Pdf




Ex 6 1 18 Solve 5x 3 3x 5 Show Solution On Number
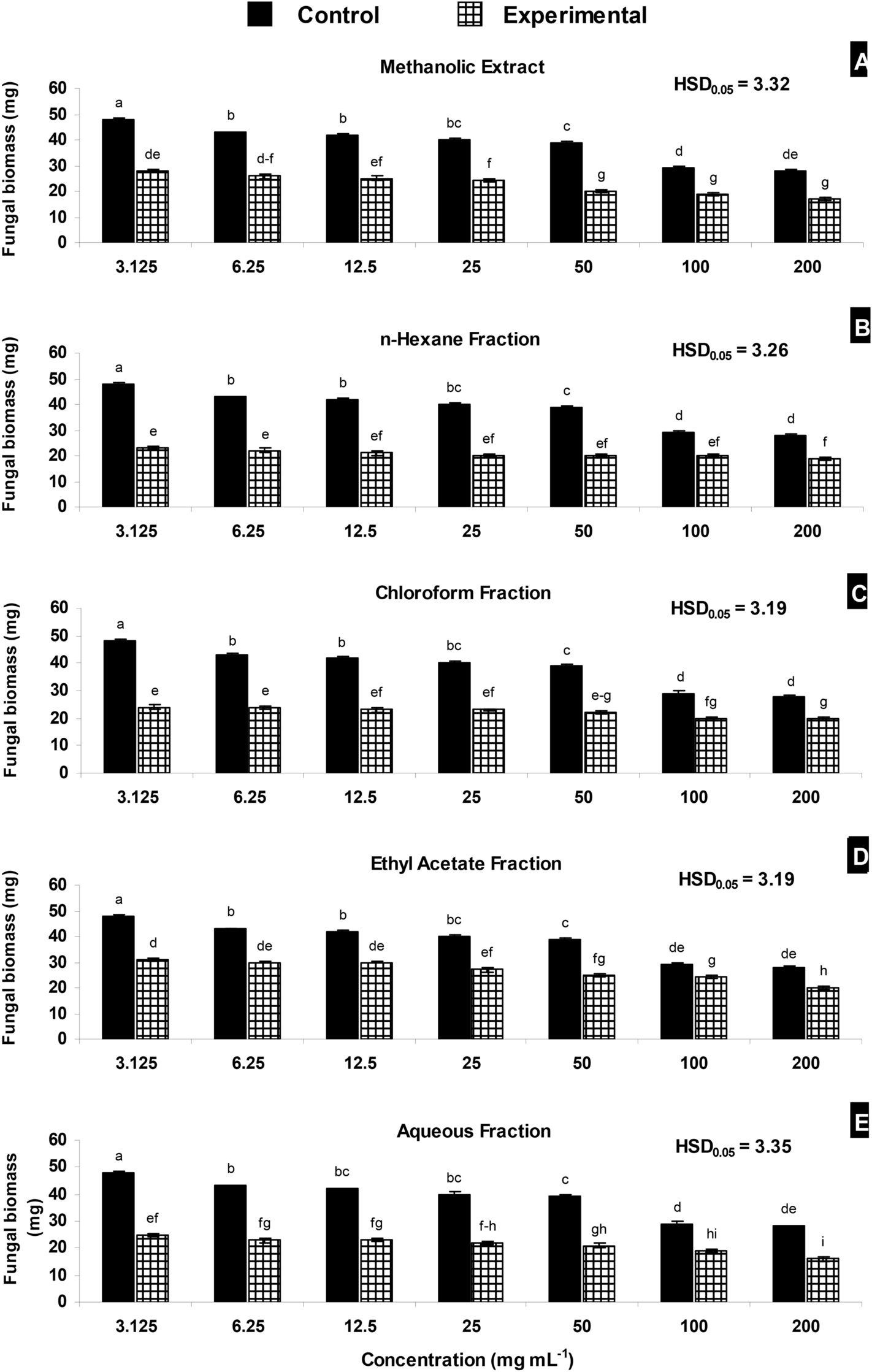



Lupeol Acetate As A Potent Antifungal Compound Against Opportunistic Human And Phytopathogenic Mold Macrophomina Phaseolina Scientific Reports
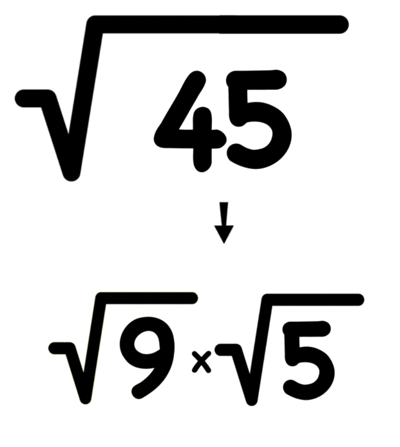



How To Multiply Radicals In 3 Easy Steps Mashup Math




Example 18 Solve 5 X 1 1 Y 2 2 6 X 1 3 Y 2 1 Examples



The Coordinate Plane



Q Tbn And9gcsy4rjtwq Ygbovdum4uzlhe8gnd0nrv0tjjyhl1cecpugesa Usqp Cau
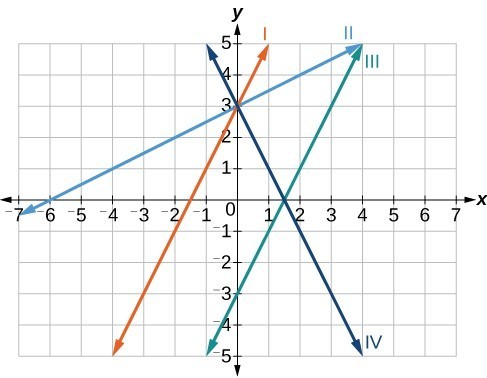



Write The Equation For A Linear Function From The Graph Of A Line College Algebra




Slope And Y Intercept From Equation Video Khan Academy
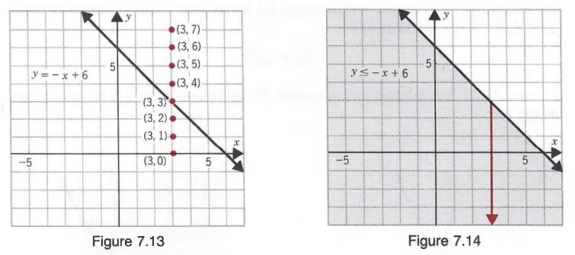



Graph Graph Equations With Step By Step Math Problem Solver




Algebra Calculator Mathpapa
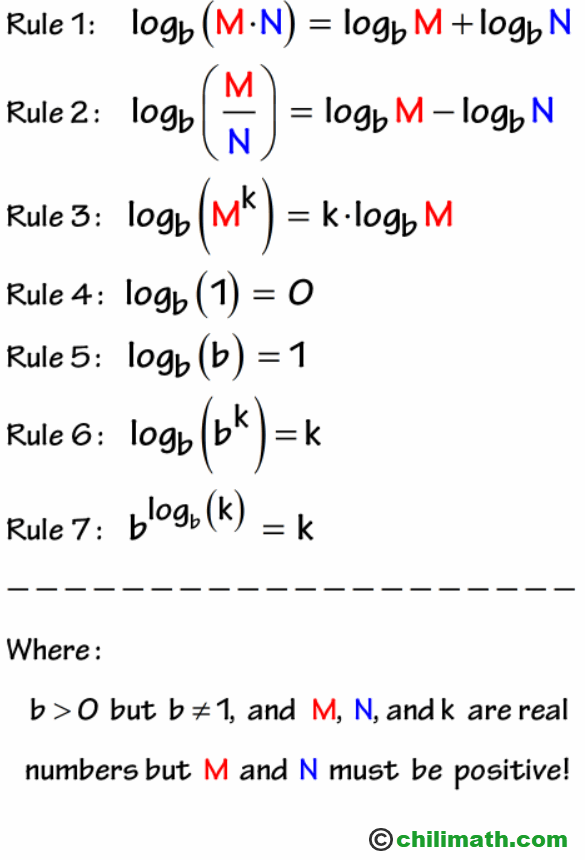



Logarithm Rules Chilimath




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




Circle Equations




Fractions To Decimals Teachertwins C Ppt Download
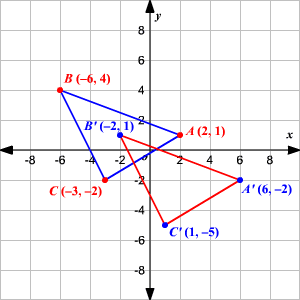



Translations




Slope Review Algebra Article Khan Academy




Long Division Calculator With Decimals
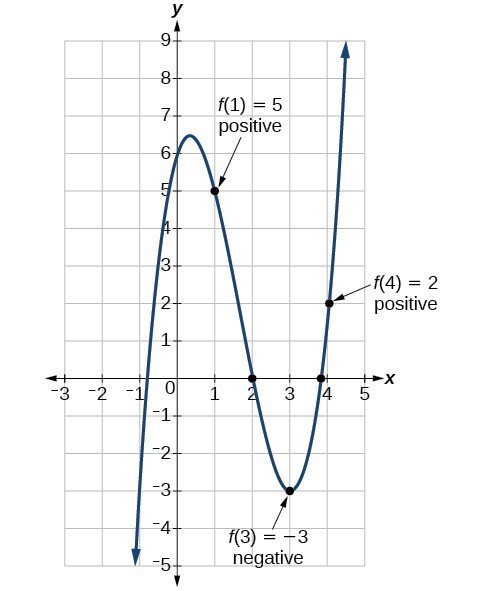



Use The Intermediate Value Theorem College Algebra




Fibonacci Number Wikipedia




Problem Set 1 Solution Studocu




Multiplying And Dividing Radical Expressions




Multiplying And Dividing Radical Expressions




Prime Numbers The Sieve Of Eratosthenes




Multiplying And Dividing Radical Expressions




Divisibility Rule Wikipedia




Solving Cubic Equations Solutions Examples Videos




Consider The Following Time Series T 1 2 3 4 5 6 7 Chegg Com



Osa Determination Of Point Of Incidence For The Case Of Reflection Or Refraction At Spherical Surface Knowing Two Points Lying On The Ray




Multiplying And Dividing Radical Expressions



Solved Find The Equation Of The Hyperbola With Foci At 0 5 And Vertices At 0 3 Plus Minus Sign Put The Equation Of The Hyperbola Wit Course Hero



1



Is X 5 A Factor Of F X X3 4x2 3x 7 Use Either The Remainder Theorem Or The Factor Brainly Com



3




Example 3 Solve X 3 5 2 3 2 Chapter 2 Class 8 Teachoo
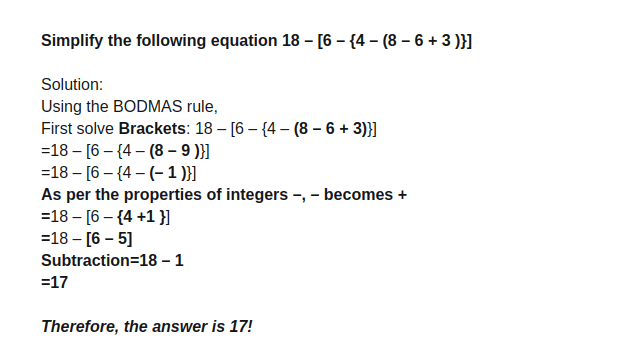



How To Solve Bodmas Questions Rules Worksheets Leverage Edu




What Is The Solution For An Equation Of A Line Passing Through The Point Of Intersection Of 2x 3y 5 0 And 7x 5y 2 0 And Parallel To The Lines 2x 3y 14 0 Quora




255 3 5 Gauthmath
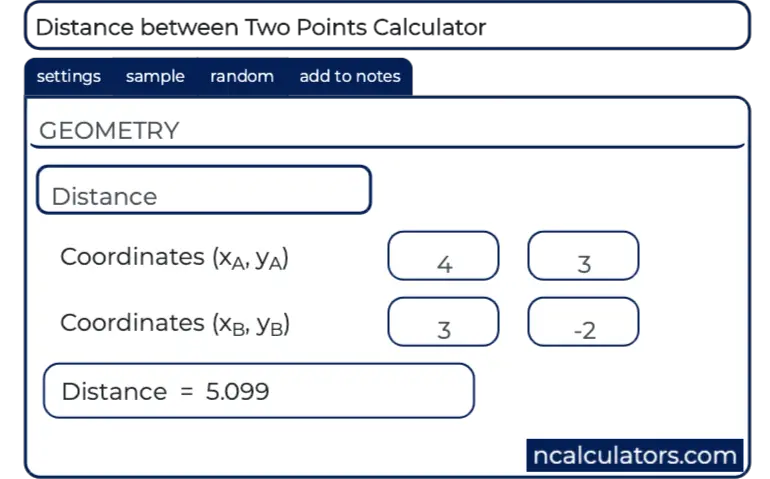



Distance Between Two Points Calculator




What Is 3 5 As A Decimal Solved
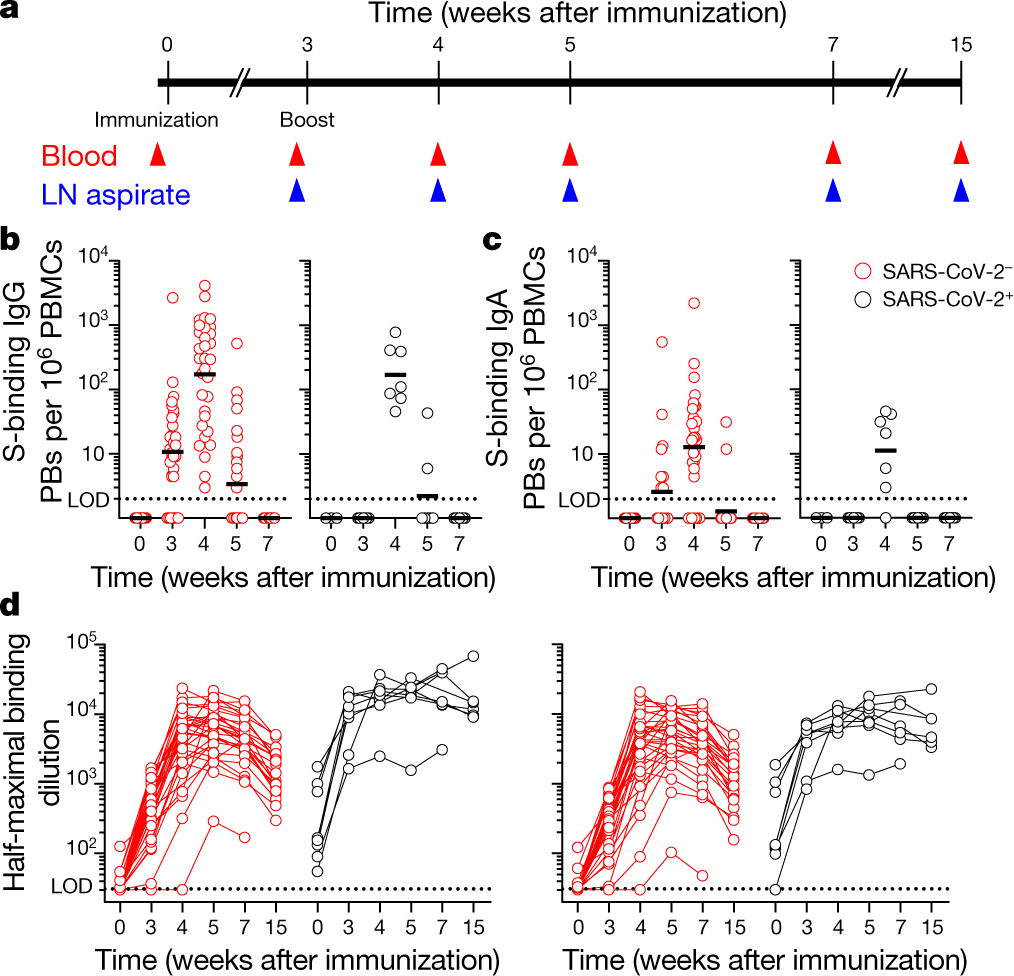



Sars Cov 2 Mrna Vaccines Induce Persistent Human Germinal Centre Responses Nature
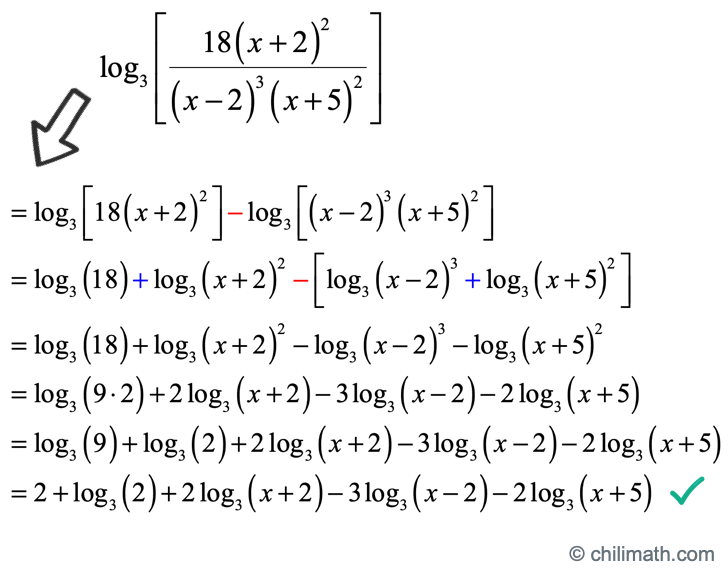



Logarithm Rules Chilimath




Distributive Property



Http Www Math Colostate Edu Clayton Teaching M2260s13 Exams Exam2solutions Pdf




Ex 12 3 7 Simplify Expressions And Find Values If X 3 A 1 B




X 2 1 5 X 3 1 4 Youtube




Using The Quadratic Formula To Solve This Equation Chegg Com
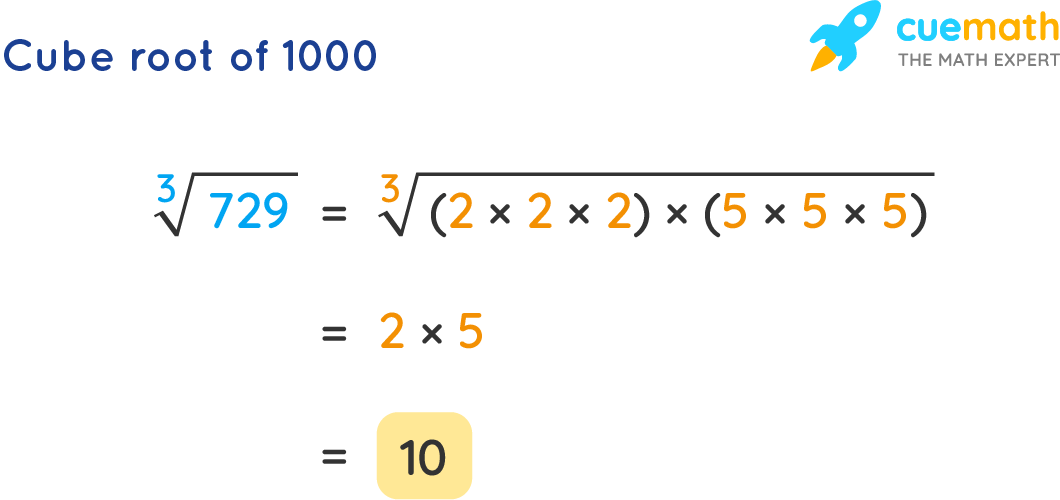



Cube Root Of 1000 How To Find The Cube Root Of 1000 Solved




Doc Math Revision Ansy Chung Academia Edu



Finding The Slope Of A Line




Misc 16 Solve Equations 2 X 3 Y 10 Z 4 4 X 6 Y 5 Z 1




How Do You Solve X 1 2 Y 2 3 4 And X 2y 5 Socratic



Factoring Trinomials Bingo
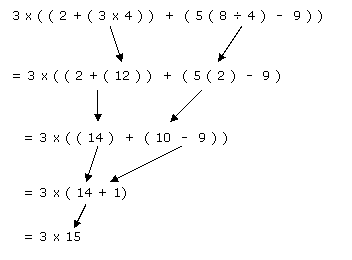



Order Of Operations




5 9 7 8 5 4 1 3 4 35 1 5 Gauthmath



0 件のコメント:
コメントを投稿